Completing forms using our PDF editor is more straightforward compared to anything. To modify 8 5 practice law of sines form g answers with work the form, there is nothing you should do - just keep to the steps down below:
Step 1: Choose the button "Get Form Here" and select it.
Step 2: So you are going to be on the file edit page. You'll be able to add, change, highlight, check, cross, insert or erase areas or words.
The following sections will frame the PDF file that you'll be completing:

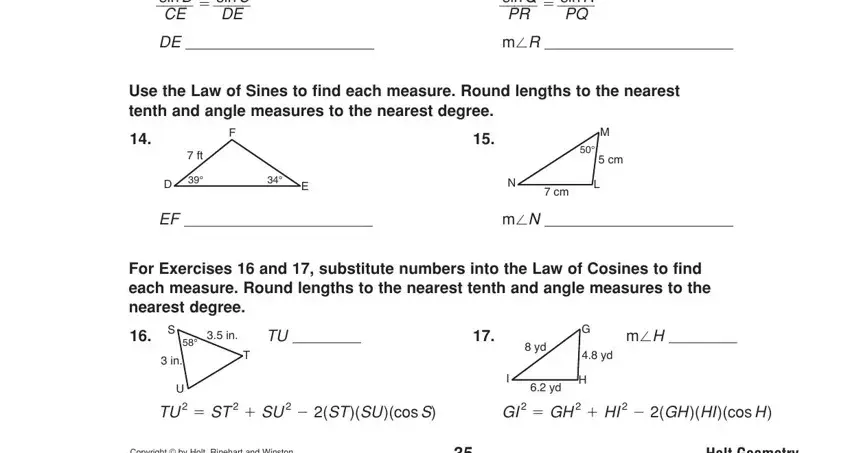
Enter the essential data in cid sin D CE, cid sin C DE, cid cid sin R PQ, sin Q PR mcidR, Use the Law of Sines to find each, cid, cid, cid, cid, cid, cid, mcidN, For Exercises and substitute, cid, and cid section.
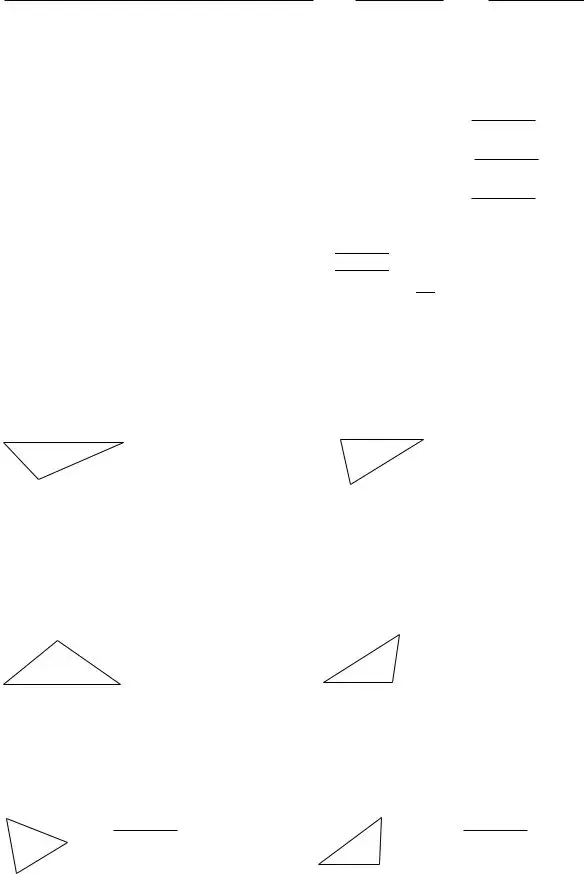
Determine the necessary particulars in the LESSON, Practice A Law of Sines and Law of, LESSON, Practice B Law of Sines and Law of, Use a calculator to find each, sin cid, sin cid, sin cid, Use a calculator to find each, sin cid, sin cid, In Exercises and fill in the, cid sin B b, cid sin C c, and For any cidABC with side lengths section.

Take the time to include the rights and obligations of the parties inside the cid, TU in, cid, cid, cid, mcidH, cid, cid, TU cid ST cid SU cid STSUcos S, GI cid GH cid HI cid GHHIcos H, cid, mcidI cid, cid, mcidM cid, and cid section.

Check the sections cosine of the angles complement, Copyright by Holt Rinehart and, Holt Geometry, Copyright by Holt Rinehart and, Holt Geometry, Copyright by Holt Rinehart and, GoanCRFcindd, and Holt Geometry and thereafter fill them in.

Step 3: After you hit the Done button, your finished file is readily transferable to every of your gadgets. Or, you may deliver it through mail.
Step 4: You can create copies of your document tostay away from any type of forthcoming concerns. Don't get worried, we do not reveal or track your data.